Quantum AI - Part 2 - The dice have been cast!

Previously, in the Quantum AI column, we have seen that quantum computing would theoretically enable some complex machine learning algorithms to be executed in a “reasonable” time (less than several years…). But what is so different about quantum computers compared to today’s computers? The purpose of this article is not to go into theoretical details but to simply illustrate – as faithfully as possible – the fundamental differences between classical and quantum computers, especially with a quantum algorithm example.

Understanding the bit concept with the coin analogy

To understand why calculations are potentially much faster in a quantum computer, let’s recall the general functioning of conventional computers. They use bits to code information and are made of electronic circuits so that, when the current flows through the circuit, the bit is worth 1, otherwise the bit is worth 0. You can also consider the electrical voltage rather than the current, the approach will remain the same. To make basic calculations with logic gates (the famous conditions “AND”, “OR”, “NOT”, etc.), we typically use transistors acting as conditional switches: when the “base” electrode is supplied with voltage, they let the current flow between the other two electrodes.

For the rest of this article, we assume that a bit is materialized by a coin. When heads turn up, we can say it codes the value 1, else, when tails turn up, it codes the value 0. There are many other possible analogies (a bulb that lights, a door that opens, etc.) but in my opinion, the coin can illustrate some quantum phenomena – described hereafter – in a simpler way.

Technical digression

The coin analogy eases the mental representation of the rotations and projections of a pure quantum state on the Bloch sphere. In this model, the coin’s heads and tails are similar to the electron spins (spin up ↑ and spin down ↓).

Now, let’s suppose we can shrink the coin size to the atom scale. At that point, its performance could be compared to certain particles and could no longer be described by the usual macro-object mechanics. Here our quantum coin materializes a quantum bit (more commonly called “qubit”) and many phenomena now come into play. I will only expose here the most important of them for the purpose of this article.

The superposition phenomenon

From a quantum point of view, if an object has two possible states then any combination of these states is a valid state. This phenomenon is often illustrated by the paradox of the Shrödinger’s dead-and-alive cat.

Let’s go back to the quantum coin: it has two possible states at rest (heads or tails up) so it could theoretically turn heads and tails up simultaneously. You can imagine the coin rests “on its edge” (in the real world, it is more complicated than that, but it does not matter seriously). Mathematically, resting on the edge is a linear combination of heads and tails with complex coefficients.

Technical digression

You may wonder why it involved some square roots of ½. Although they are not necessary to understand this example, these coefficients are interesting because they refer to probabilities when squared. The coefficient in front of heads (respectively tails) is the probability amplitude of “seeing” the coin landing on heads (respectively on tails) when it collapses on the side. An amplitude just has to be squared to be turned into a probability. An amplitude can also be negative or even complex (in this case, we take the squared norm to assess the probability). What does it mean to have negative (or even complex) amplitudes? It is simply a rotation around the vertical axis. For example, -1 (= exp (i.Pi)) is a 180-degree rotation.

Conclusion: qubits are complex combinations of 0 and 1. By analogy, a quantum coin can turn heads or tails up simultaneously, by resting on the edge.

The wave packet reduction (~ the wave function collapse)

In the macroscopic world, when a coin rests on its edge, the slightest disturbance (shaking, sneezing, etc.) makes it collapse, with generally 50/50 probabilities for heads and tails results. At the quantum scale, it is so sensitive that it is actually impossible to “see” the coin on the edge because the light itself makes it collapse immediately. To make the coin rest on its edge, you need to isolate it in a perfectly hermetic black box, without any interaction with you or the environment. Under these strict conditions, the coin will evolve spontaneously on its edge, even on “inclined” edges (which would defy the laws of gravity on our scale, but it doesn’t matter). And as soon as you open the box, the coin will collapse instantly, with 50/50 probabilities for heads and tails results. It could also be non-symmetrical probabilities depending on the inclination on which the coin was resting just before opening the box. This phenomenon is called wave packet reduction, also known as wave function collapse (I personally prefer the latter insofar as it describes more the very great instability of the system as well as the idea that the potential realities eventually collapse on the observed reality).

Conclusion: to make the quantum coin rest on its edge, you must neither look at it, nor interact with it. Even if it may rest on its edge theoretically, it is actually impossible to “see” it in such a state; you can only see it rested on heads or tails, after collapsing.

The entanglement phenomenon

Looking at some articles, the entanglement is a phenomenon that has been overjoyed and fed many delusions. It is related not to one but to two quantum coins (or more) and stipulates that, if your two coins has been created under very specific conditions, then their respective fates are linked. For instance, if you stick two coins on their edge (like Siamese twin coins), then they are part of a single and undividable system. We can say here that our coins are “entangled”.

If one is resting on heads, the other is necessarily resting on tails. When you toss this set of two glued coins, the two initial coins necessarily land on opposite sides (one on heads, the other on tails). But the very strange thing is that their osmosis will carry on even if we tear them off. Imagine that we finally separate the two coins and that we enclose the right one in an isolated black box.

Let’s suppose now we flip the left one. In this case, if the left coin lands on heads, then, if you open the black box, the right coin will be resting on tails… and vice versa! And this will be obtained without anyone having touched the right coin!

The entanglement has fascinated many authors and scientists. As the “interaction” of the left coin on the right one is instantaneous, regardless of the distance separating them, some people reckoned it might be a way of teleporting information, or even time-traveling. No worries, this is rather inaccurate. No information can strictly teleport (meaning travel faster than light). Indeed, the action between the two coins may be immediate, we never know in advance the result of a coin flipping. So the result of the other coin (in the black box), cannot be transmitted in advance to someone else… for its result will change at the very last moment, when the coin flipping ends. An information is not a superposed system, only a actual measure.

Technical digression

Likewise, you unfortunately cannot use this phenomenon to reach the limits of causation. A 2012 study (E. Megidish, et al.) tells that two photons can be entangled even if they have never coexisted in time. This is made possible in this experiment by using four photons and by performing an entanglement swapping between two of them. The issue here is the interpretation of events temporality which, in my opinion, is more a matter of special relativity than quantum mechanics. Rather than time-related entanglement, it would be more correct, in my opinion, to talk about entanglement inheritance or exchange over time.

A first example of a quantum algorithm: the Deutsch-Jozsa algorithm

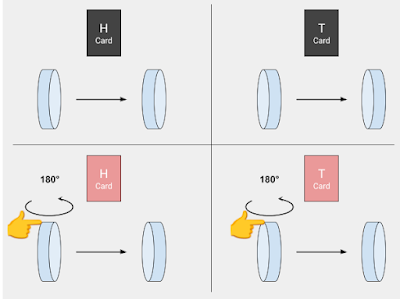
Now it’s time to concretely understand why some quantum calculations are more efficient than their classical counterparts. To do this, let’s play a riddle. You have a coin (an information bit). In front of you is a magician who has two face-down cards (from a traditional deck), marked “H” and “T” (referring to your coin Heads and Tails). The magician’s cards act on your coin depending on the side it is resting. The game goal is to find out whether the magician’s cards are the same color or not .

To perform it, you can present your coin to him with heads or tails up. If the coin turns heads up, the magician uses his H card as follows: 

• If the H card is red, he flips your coin over to make it rest on tails 
• If the H card is black, he does nothing, it leaves the coin heads up 

Likewise, when you present the coin with tails up, the magician will then use his T card : 

• If the T card is red, he flips your coin over to make it rest on heads 
• If the T card is black, he does nothing, it leaves the coin tails up 

The important thing is that, in any case, the magician must give your coin back after (on heads or tails), depending on the color of the corresponding card.

With a classic piece, solving the problem is fairly intuitive. You present the coin heads up; the magician acts on it with his H card: if he flips the coin over, then you know that the card is red… otherwise it is black. Then, you retry with the coin tails up. If the magician flips it over, then his F card is red, otherwise it is black. By presenting the coin twice in a row (once on heads, once on tails), you have the answer every time. You carried out two operations to achieve your goal (since you presented the coin twice to the magician).

But what happens if we now use a quantum coin? In this case, you are exceptionally allowed to present the coin… on its edge! Problem: the coin is supposed to collapse immediately on heads or tails. Remember, when we talked about the wave packet reduction, to make the coin rest on its edge, you need to left it quietly in a black box without any interaction at all. In fact, there is another phenomenon which expands the wave function collapse and allows a little flexibility: it is the quantum decoherence phenomenon. With it, it is actually possible to manipulate a quantum coin only for a very short period of time (generally around a few microseconds or milliseconds for the best quantum computers). After what, the coin is forced to collapse into a “classical state”: heads or tails up. As part of the problem, we will assume that the magician has powers that allow him to work long enough on the coin before it collapses on heads or tails.

Let’s go back to our game. How will the magician use his cards if you present him a quantum coin on its edge? In fact, showing him a coin on its edge means you show him both sides simultaneously. In this case, the magician is forced to use his two cards in the same time: if the H (or T) card is red, he flips the coin over; otherwise he does nothing. But what does it mean flip the coin over when it is resting on its edge? Well, here the coin performs a 180-degree rotation around the vertical axis, like a spinning-top.

Then the magician must give the coin back to you. But don’t forget, if you look at the coin, it collapses instantly on heads or tails (with 50/50 probabilities). But you can ask the magician to push the coin on the right side before returning it.

Well, here we are, with this trick, you can know, with a single coin presentation (a single measurement), whether the cards are the same color or not. Indeed, if the magician returns the coin head sup, then the cards have different colors, and if he returns it tails up, then the cards have the same color. Not convinced ? Let’s see the results in detail:

So we did one calculation instead of two (we presented the coin only once to the magician). What a performance! Okay, this basic example does not show a real improvement. But in the general version of this algorithm, you can play for example with 10 coins. In this case, the magician will have 1,024 cards which will act on all possible combinations of heads and tails. In this game, either all of the magician’s cards are the same color, or half is red and the other half is black. The goal is the same: to know the distribution of the magician’s deck. With classical coins, you will have to make between 2 and 513 attempts to find out if his deck of cards contains as much red as black. With quantum coins, you will only need one attempt because you will present your 10 coins on their edge… Here it seems to be more interesting in terms of computing acceleration!

This algorithm has no practical utility even if it roughly shows why a quantum coin can combine information (heads and tails) to reduce the number of operations and then save time. But for more sophisticated algorithms (eg quantum simulated annealing, Shor, Grover, Harrow-Hassidim-Lloyd algorithms), the use cases are very concrete: (de/en)cryption of sensitive data, search in an unsorted database, problems optimization, weather forecasts, molecular simulations for drug discovery, etc.

To sum up, quantum computing relies on the superposition of states and the entanglement of qubits to inherently perform parallel computing (without having to distribute processing on different machines). It also includes the concepts of decoherence time and wave function collapse which are necessary to go from a quantum operation to a real and useful measurement! All the complexity for our coders and physicists is therefore to identify the algorithms (and more specifically some specific operations, see the first article on quantum AI) whose formalism can be adapted to introduce the aforementioned quantum phenomena in order to accelerate the processing time. Finally, let’s remind that the benefits of quantum computation do not apply to all algorithms and that the performance gain is not always significant compared to computations on conventional computers. Today, we do not have true stable quantum computer which is actually marketed. But things should change quickly, when high-ROI quantum use cases increase within companies…

____

This article is part of a column dedicated to quantum AI. Find all posts of the same theme:

Part 1 – Ending impotence!

Part 2 – The die has been cast!

Part 3 – Rise of the AIs

Part 4 – The key role of DataOps

A. Augey

Also published in Saagie's company blog: https://www.saagie.com/blog/quantum-ai-part-2-the-dice-have-been-cast/